arraylists introduction

ArrayList is a dynamic, ADT data structure.

Abstract data types (ADT)

This is a model description of a data type that is defined by the type's behaviors and operations. This is similar to a Java interface, where there are operations (methods) that can be utilized, but the implementation is abstract.

An example of the List ADT:

• addAtIndex(int index, T data) adds an item to the list
• removeAtIndex(int index) removes an item from the list
• get(int index) returns data
• isEmpty() returns whether the list is empty
• clear() resets the list configuraiton with no data
• size() returns the number of data currently stored in the list

The List ADT is comprised of different variations of ArrayLists and LinkedLists.

ArrayLists

• a type of List backed by an array
• Each of Java's ArrayLists will have to store the object, for primitives this requires an object wrapper

Example in Java:

// ArrayList in Java is from package `java.util`
// The data type must be an `Object`
// generic typing is implied from the declaration statement

ArrayList<String> list = new ArrayList<>();

Dynamic allocation

• an arraylist is an abstraction / a wrapper for an array
• these are resized automatically by the implementation without users knowing
• this is dynamically allocated memory because the array is reallocated and copied when more space is necessary
  • the resizing is still considered O(n) because it is using an array as an underlying component
  • resizing is still a limitation because of the array structure

Arraylist terminology

• the size of the data structure is the # of non-null pieces of data being stored in it
  • this is typically stored in a variable
• the capacity of an arraylist is the # of data that can be stored

Ex ArrayList:

// This has a size = 5
// and a capacity = 8
[a][b][c][d][e][][][]

Arraylist requirements

• data must be contiguous
  • there cannot be null spaces between the data
• data must be zero-aligned (must start at index 0)
• for efficient operations the size should be stored
  • the index size gives us access to the next empty spot in O(1) time

Ex ArrayList:

// data is not contiguous
[b][a][][d][][][][]

// data is contiguous but not zero-aligned
[][b][c][d][][][][]

// properly done
// size = 5
[a][b][c][d][e][][][]

Adding to an arraylist

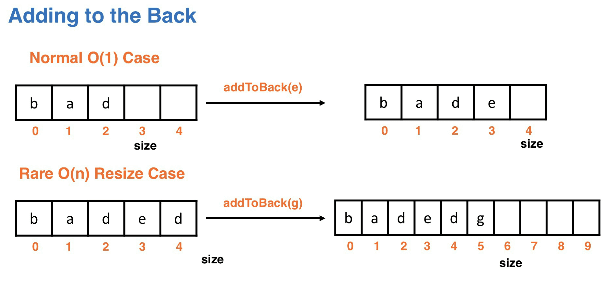
• we can add to the back in O(1) if resizing is not needed
  • this is due to knowing the size ahead of time
• adding to the back of an arraylist and doing a resize is considered worst-case
  • once the capacity is exceeded we are facing a cost of O(n)
  • the cost of adding is "pessimistic" because the resize step is considered rare
• amortized analysis states that looking at the cost over timer ather than the cost per add operation
  • this implies that adding to the back will still be O(1) if we used amortized analysis
  • because we are just repetitively adding to the back during resize, it would be repetitive single operations "n" times

// normal O(1) case
// addToBack(f)
// size 5 -> size 6
[a][b][c][d][e][][][] -> [a][b][c][d][e][f][][]

// rare O(n) resize case
//      this requires a resize and each of the data pieces
//      must be copied over
// addToBack(f)
// size 5 -> size 6
[a][b][c][d][e] -> [a][b][c][d][e][f][][][][]

Adding elsewhere

• adding at an arbitrary index is not the "back", it is O(n)
  • we have to add at a position then copy each of the index values to their new positions
  • all data must be shifted, which would then open the cell to insert the data

// addAtIndex(1, f)
// all data must be shifted 1 cell at a time
[a][b][c][d][e][] -> [a][f][b][c][d][e]

Remove operations

• removing from the back is O(1)
• removing from an arbitrary index not at the back is O(n) due to data shifting

// removeAtIndex(0)
// all data must be shifted 1 cell at a time
// down 1 index
[a][b][c][d][e][] -> [f][b][c][d][e][]