big o notation
Purpose
- analyzing efficiency in both time and space efficiency
- measurement that is platform/hardware independent
- high level of description of the algorithm without the implementation
- performance scales in relation to the input sizes
- implementation states how well an algorithm scales given the inputs
- complexity of an algorithm is how efficient the algorithm is in terms of input sizes
High level description
The high level desc. describes an algorithm in what it wishes to accomplish.
Primitive operations:
- assign a value
- arithmetic operation
- comparing some entities
- method calls or returns from a method
Primitive operations execute in constant time
- we count the # of primitive operations as a way of determining the efficiency
Efficiency as a function
Measuring efficiency as a function using the representation of the algorithm.
Creating some function f(n) representing the function on an input of some size n.
Three cases when determining a function:
- worst-case - the algorithm running with the worst set of data, worst performance
- best-case - the algorithm running with the best designed set of data, fastest performance
- average-case - somewhere between and difficult to compute
we always want the most accurate, worst-case analysis for Big-O
Big-O Notation
This is a functional representation of the algorithm's efficiency.
- Denoted with: O(f(n)) noting the algorithm scaled on the size of the input
- This represents an upper bound, but we want the most accurate upper bound
- Ex: Everything in this course is O(n^4), but this isn't descriptive of performance
- other measures: o(n), big-omega of n, big-theta of n
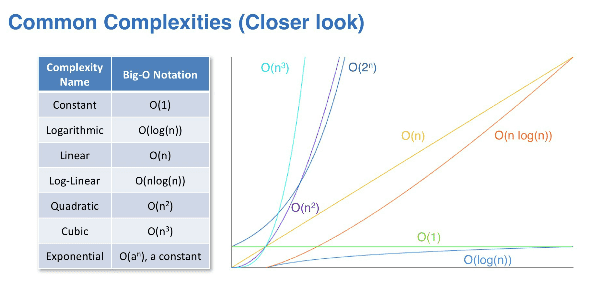
Common complexities
These complexitites are common and can be easily found graphed next to each other.
ex: 100 ops with 1000 inputs
| Complexity name | Big-O notation | N = 1000 |
|---|---|---|
| Constant | O(1) | constant |
| Logarithmic | O(log(n)) | 0.09966 |
| Linear | O(n) | 10 |
| Log-Linear | O(nlog(n)) | 99.66 |
| Quadratic | O(n^2) | 10,000 |
| Cubic | O(n^3) | 100,000,000 |
| Exponential | O(a^n), a constant | 1.07 x 10^299 |
We want to stay closer to the complexities at the top of the table, rather than the bottom
- complexity increases as we go down the table
Primitive operations
- primitive operations - defined as basic operations like memory and reference management, comparisons, basic arithmetic
Asymptotic notation
We will largely stick to big-o notation and denote hte tightest upper bound on performance.
- O(f(n)) : The algorithm's long-term performance cost is upper bounded by f(n). This is the most common asymptotic notation that you will see, and you will become very familiar with it in this course.
- o(f(n)): The algorithm's long-term performance cost is significantly upper bounded by f(n). This measure is often used if we want to emphasize how small a quantity is or how slowly it grows. For example, in many numerical methods, we may want to approximate some quantity within a reasonable error. It's common to denote the error term using Little-oh notation to show that the error term grows slowly.
- Ω(f(n)): The algorithm's long-term performance cost is lower bounded by f(n). This measure is interesting because it requires us to flip our line of thinking. Rather than thinking about how badly our algorithm can perform like in Big-O, this measure is often times used to tell us what performance costs are reasonable to begin with for a problem. If we have an algorithm that has time complexity O(n4), we may think to ourselves "yikes...," but if the problem the algorithm is solving has a complexity of Ω(n4), then we realize that our algorithm wasn't so bad, it's just that the problem is very hard to solve!
- Θ(f(n)): The algorithm's long-term performance cost is both lower bounded and upper bounded by f(n). In other words, it is both O(f(n)) and Ω(f(n)). Not all algorithms will have a valid Big-Theta since it requires the algorithm to have consistent enough behavior that we can sandwich it from both above and below.
Big-O conventions
These are common conventions and things to pay attention to in the course.
- drop constant factors:
- constant factors grow insignificantly as we go to infinity
- ex: O(5n) -> O(n) O(0.5n^2) -> O(n^2)
- constant factors grow insignificantly as we go to infinity
- drop lower ordered terms
- this is because the fastest growing term will dominate as you approach infinity
- ex: O(n^2 + 1000n - 3) -> O(n^2) O(3n + 2log(n) + nlog(n)) -> O(nlog(n))
- this is because the fastest growing term will dominate as you approach infinity
O(1) - constant time complexity
Regardless of the size of the data set, the operation can be executed in the same amount of time every single execution.
- Performance does not scale at all with input size
- Ex: Given an array of length n, returning the first element is O(1)
- this is because we can always immediately access the first element
O(n) - linear complexity
Performance scales proportionaly with the input size.
- Ex: Given an array of length n, summing up all elements in the array
- This grows linearly with the size of the arrays, based on the number of inputs (n)
O(log(n)) - logarithmic complexity
We did not specify a base, but typically in CS it will be base 2. The base for O(log(n)) ends up being a constant factor.
- The performance scales logarithmically with input size.
- Ex: given a sorted array of length n, performing a binary search.
Constant factors: importance
Big-o is a measure of how performance scales as the iput grows towards infinity. Constant factors do not grow, they are not needed to depict growth, and lower order terms are dominated by the higher order ones.
Ex: Algo A has a time complexity of O(n), B has complexity of O(n^2)
* When looking at A you can usually assume it would be faster; however, if given the number of primitive operations:
* A performs 1,000,000,000n operations while algo B performs 2n^2 operations on a typical use case
* Unless n >= 5 billion, B will outperform A in terms of # of operations