stack adt lesson

The Stack ADT is a model for data that behaves linearly. These are fundamental to computer science and are found in many implementations.

Linear abstract data types (ADT)

What makes it linear?

• Finite collection of objects
• A collection is linear if each object has:
  • one immediate predecessor
  • one immediate successor
  • exceptions are the first and last object of the collection

Abstract data type, ADT:

• The data structure that is a container with a finite number of objects (size)
• There is a relationship between the objects being stored
• The low level details are hidden with a "high level idea"
• Behavior defines the data abstract data type
  • operations and methods used more closely define the abstract data type

Potential backing data structures for a Stack ADT

The backing of a Stack ADT can be done in multiple ways.

Arrays or LinkedLists are the typical backing data structures used.

Time complexities review

Time ecomplexities of an Array, Singlylinked, or Doublylinked lists.

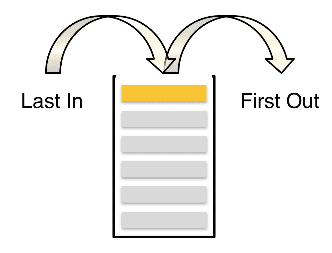
What is a Stack?

Stacks are defined by their behavior. The behavior is as follows:

• To add to the stack we push data to the top of the stack
• To remove data from the stack we pop off the top of the stack
• Stacks are called LIFO - last in first out
• Stacks only have access to the most recently added item
  • This ADT is not made for searching or accessing beyond the element that was last added

Stack supported operations

• a void push(x) that pushes to the top of the stack
• a x pop() that pulls off the top of the stack and returns the element
• a x peek() or x top() method that returns the element on top of the stack without deleting/adding
• the boolean isEmpty() methods that check the stack to determine if it is empty
• the void clear() method that clears the stack and returns nothing

Stack unsupported operations

• seraching within the stack for data
• Arbitrary index access
• Arbitrary add/remove of data at indexes

Stack examples

A can of potato chips is an ideal example

• The undo button in a word processing application
• The stack of apps open on a smart phone

The Call Stack

Method calls (and recursion) exhibit Stack behavior. Method calls behave as:

• When a method is called, the current method that is active is paused, then the new method begins execution
• When a method call terminates (returns) the method call that was previously active unpauses and continues exectuion from where the method call was made

This is remarkably similar to the Stack behavior.

For the method call stack, making a method call means pushing a method call onto the stack with any parameters along with the information needed to pause and begin execution.

Terminating a method call does a pop from the method call stack.

The method currently executing is whatever is on the top of the call stack.

This explains the Stack traces that are dumped when method calls have errors, in Stack order.

Infinite recursion results in a StackOverflowError.

Backing implementations for the Stack ADT

The backing structures do not define the Stack, just the methods and behaviors.

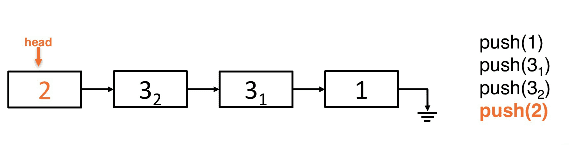
Linkedlist backed stacks

A singlylinked list implementation

• When the list is empty, we know that the head points to null and is known
• When pushing to the top we addToFront() for each item and push the list

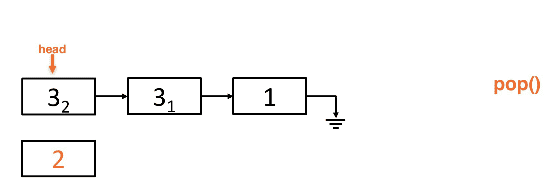
Popping from the list:

Performance of a Linked-List backed Stack

• No tail pointer
• Stacks ar elightweight and as simple as possible
• Singlylinked lists are best, they don't need as much memory
  • Memory overhead of a Doublylinked list would be more intensive and overkill
• Each Stack operation for a singlylinked list implementation is O(1)
• You can technically implement this using addToBack() and removeFromBack()
  • You would need to use a Doublylinked list to have a tail to make this O(1)
  • This would also be subject to traversal to remove the nodes when resetting the tail

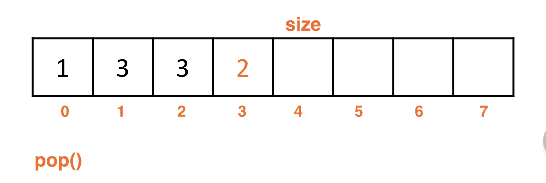
Arraylist backed stacks

Array backed stack implementation

• Rather than check the array's head we check the size
• Adding using a size variable using addToBack() allows us to push in O(1)
  • Adding to the front with addToFront() would be an O(n) because we have to traverse the array
• By doing operations for adding/removing with the back (aka, addToBack() and addToFront()) we can keep O(1) time
• Pushing onto the stack is an amortized O(1)* operation because we still encounter resizing

An Array backed stack implementation:

Clearing an Array backed stack:

• Resetting the size to 0 would technically clear the stack
  • Java cannot garbage collect the data that is abandoned
• Using an iteration to manually reset each data point to null would be O(n) and inefficient
• Reassigning the backing array to a new array, then reset the size to 0
  • This allows Java to use garbage collection on the array and is done in O(1)

Stack implementation time complexity

This uses some amortized big-o complexities, noted with *.