adding to a bst

Adding to a BST has similarities to searching; however, if we need to restructure the tree it will be a bit harder than doing a search.

BST search vs. add

The methods for searching and adding are both recursive methods that will search for data via traversal.

• To maintain the structure of a BST we have to add only as leaf nodes
  • Insertion into the middle of a tree is very difficult and has no real way to reconcile the structure
• Note: Adding data to an empty tree puts data in at the root
• Data is added at null values so long as it is not already a node

BST search vs add chart:

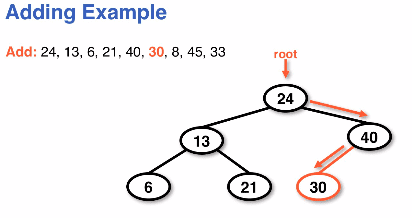
Adding nodes to a BST example:

• The above example utilizes a recursive search to check each node

Changing the tree structure

When implementing the add method we use pointer reinforcement.

• Adding a node changes the parent node's left or right pointers, not the node that is being added or removed

• pointer reinforcement - For each call use the return field to restructure the tree

  • Return the node that should be in the direction of traversal
    • If you traverse left, return what should be the left child
    • If you traverse right, return what should be the right child
  • Set left/right pointer to what is returned
  • This changes the restructuring to the recursive call of the parent rather than the child

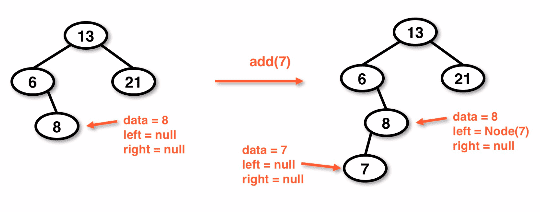
• lookahead method - The recursion is done at one level ahead by keeping track of the parent node rather than the node being added or removed

  • This never actually reaches a null node
  • It just checks to see if the child in the direction to travel is known or null
  • Example: If a child is null, then we can add there
  • Works for simple restructuring operations like add, for more complex structures this becomes difficult

Adding to a BST diagram:

Pointer reinforcement

The add() method for a BST using pointer reinforcement is a public wrapper method that implements a private method. This is used to keep the method from being changed.

The recursive method checks for 3 cases:

1. If the cursor is null
2. If the data is less than the current data (go left)
3. If the data is greater than the current data (go right)

• Node: When exiting the helpe rmethod once a node is added we return the current node at the end
  • This reinforces the pointers that were not changed once the new node is added

Pseudocode for add():

public void add(int data):
    root <- rAdd(root, data)

private node rAdd(Node curr, int data):
    if curr == null:
        size++
        return new Node(data)
    else if data < curr.data:
        curr.left <- rAdd(curr.left, data)
    else if data > curr.data:
        curr.right <- rAdd(curr.right, data)
    return curr