binary heaps

Binary heaps are the most common form of heap structure. There are more types; however, often times when discussing a heap it will be a binary heap.

Heaps are another binary tree type with an additional property completeness.

This property lends itself to an array implementation which is typically faster at a low-level when compared to a tree node implementation.

Heaps have a different order property than BSTs. This order property changes how we look at things like add/remove operations.

Heap characteristics

Heaps are a binary tree, but not a binary search tree.

• Have the shape property of a binary tree, every node can have at most two children
• Must be complete (see below screenshot)
  • This is easy to implement with an array
• Order properties of the heap characterize the type:
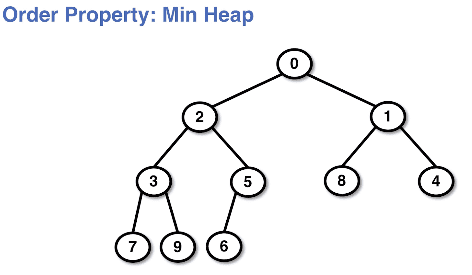
  • min heap - the smallest element in the data set is the root
    • The data in the children are larger than the data in the parent
    • There is no direct relationship between the siblings or two children
    • The data in every parent is smaller than it's children
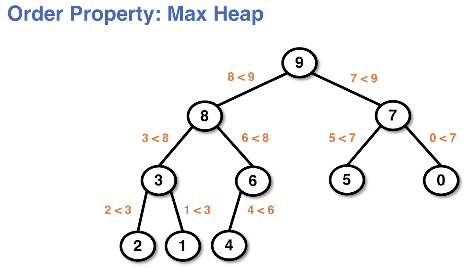
  • max heap - the largest element in the data set is the root
    • The data in the children are smaller than the data in the parent
    • There is no direct relationship between the siblings or two children
    • The data in every parent is larger than it's children
• When implementing a heap with a backing array we begin the indexing at index 1, omitting index 0

Example of complete and incomplete trees:

Min heap example:

Max heap example:

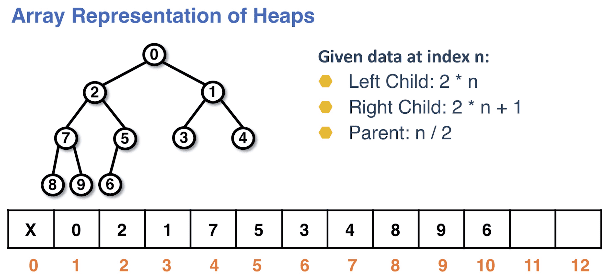
Array representation of heaps

The data is placed in a heap based on a level order traversal.

The min heap is illustrated within the array, wherein the backing array has no gaps and is complete. This allows us to:

• Compute the indexes of a parent and its children
• The backing array will not have gaps
• Given a node n we can easily find the left and right children

Finding children given an index n:

• Left child: 2 * n
• Right child: 2 * n + 1
• Parent: n / 2

Array representation of heaps:

Heap use cases

• Designed for accessing the root
• Not designed for arbitrary searching
  • No better than searching in an ArrayList: O(n)
• Often used to back a priority queue
  • This is because they always keep the largest or smallest item at the root, O(1)
  • Ex: Emergency room waitlist