binary search tree (bst)

A type of binary tree with the same properties but enforce a data order property.

Properties

A binary search tree enforces order:

• The left child data is less than the parent data
• The parent data is less than the right child's data
• All of the data on the left sub tree must be less than the data in the parent node
• All data in the right sub tree must be more than the node

Example of a valid BST:

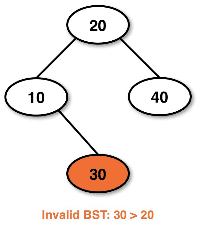
Invalid BST example:

Implementing and efficiency of BSTs

• In Java the data in a BST must implement the Comparable interface
  • This must have the compareTo method
• Motivation for binary search
  • Each comparison tells you the data is to the left or the right
  • We have to search half the data, rather than all of it
  • This is an O(logn) runtime
• Performance depends on the shape of the tree
  • Time complexity for a degenerate tree (aka a linkedlist) is O(n)

Traversals

Traversals are categorized into two groups, depth and breadth searches.

Depth traversals (stack based)

Depth searches travel down the tree, like going down a rabbit hole. These follow a path or branch as deep as it can go until it reaches a null child.

Examples:

• Preorder traversal
• Inorder traversal
• Postorder traversal

Breadth traversal (queue based)

Breadth searches travel one level at a time, these explore one step away from the root, then two steps away, etc.

Example:

• Levelorder traversal