binary trees bst

Binary trees are a tree that has a shape restriction, nodes can have at most two children.

Binary Search Trees (BST) are binary trees with an imposed order property.

Properties

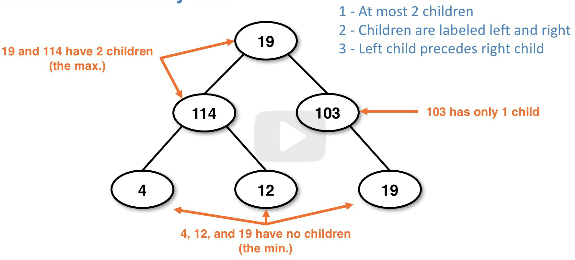
The binary tree properties required to adhere to this classification:

1. At most 2 children per node
2. Children are labeled left and right
3. Left child precedes right child

Example binary tree with definition and labels:

Node information

• data and pointers to the left and right node
• Other potential node information:
  • Parent reference
  • Depth
  • Height
• Information varies based on the need of the shape and type of the tree

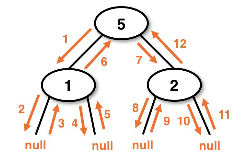
Example Node diagram:

Shape properties for binary trees

A tree is considered to be full:

• Every node except for the leaves has 2 children
  • Every node should have either 0 or 2 child nodes

An example Full Tree:

A tree is considered to be complete:

• If all of the levels are completely filled except for the bottommost level
  • The bottom level of leaf nodes is filled in left-to-right, with no gaps between nodes
• When trees are complete they are easier to back with a raise

An example Complete Tree:

A tree is considered to be degenerate:

• If all nodes only have one child reference, except for the leaf which has no children
  • This is considered the worst binary tree, it is basically a linked list
  • With this we don't have nice traversal, we're stuck with O(n)

An example Degenerate Tree:

Nodes

• References to other child nodes
• Can reference an actual node or null
  • Some implementations do use dummy nodes

Iterating through a binary tree

To iterate we use a recursive method to traverse until we find a null node

• The below implementation does not use a parent reference, which frees memory
• Once we return from the recursive call we're back at the same point in the call from its parent

// We can traverse on each side until finding null
// this doesn't require a parent reference
// which frees memory
public void traverse(Node node) {
    if (node != null) {
        traverse(node.left)
        traverse(node.right)
    }
}

An example traversal pattern using recursion: