buildheap algorithm

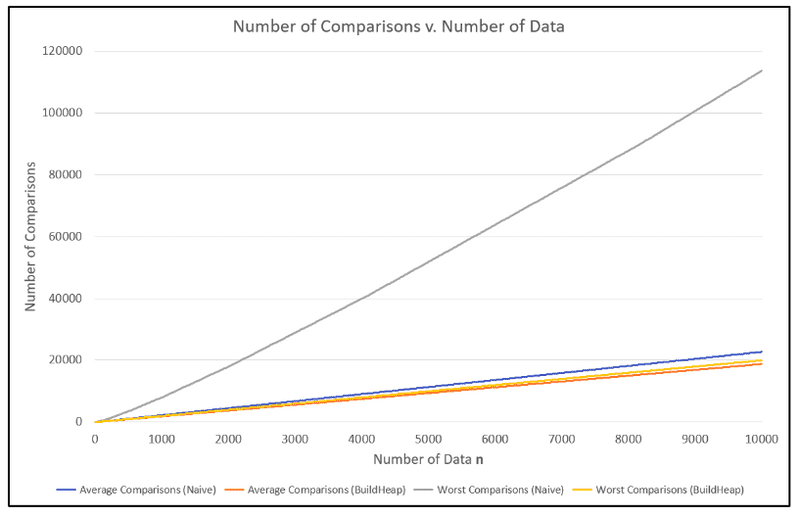
The buildheap algorithm constructs a heap in linear time. This is an improvement over the naive implementation of adding one elemnt at a time in O(nlog(n)).

The idea uses a buildheap subroutine quite heavily from the remove operation.

Problem description

• input - unsorted, unordered array
• problem - construct a heao from the input
• possible solution - use the add method to add all data to an empty heap one by one
  • adding to a heap is O(log(n))
  • we add to the heap n times
  • this solution is O(nlog(n))
  • this would be improved with an alternative approach

Validity of down-heap

If we have valid sub-heaps as children we can take advantage of the down-heap by understanding that we can down-heap into valid sub trees.

Buildheap algorithm

Build heap properties:

• shape property - put the data in as presented

• order property:

  • look at sub-heaps
  • down-heap through valid subheaps

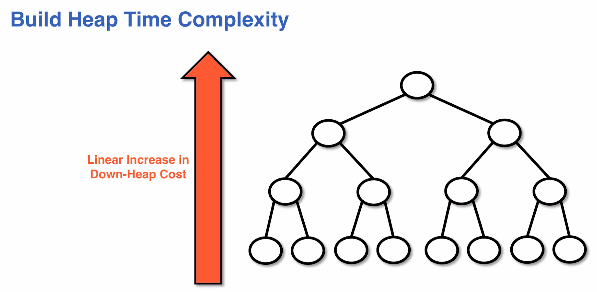
• Ensuring that the shape property is enforced and using down-heaps can reduce our construction time

• Building needs to be done from the bottom up

• Note: We iterate through the index using n / 2 where n is the size

  • This allows us to reduce the number of down-heap operations by avoiding looking at children
  • A down-heap helper method should be implemented generally for any index so it can be reused

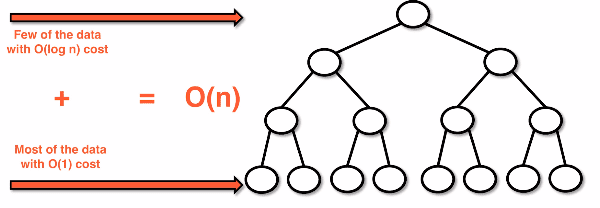
Buildheap algorithm efficiency

• Down-heap is O(logn)
• Building a downheap does n/2 operations
• The build-heap algorithm is O(n)

Linear increase in down-heap cost:

Cost differences in down-heap costs:

Number of comparisons v. number of data in down-heaps: