summations in discrete math

An important operation in numerical sequences is adding terms. This is interchangeably called series or summations. The summation notation is useful when counting operations in things like loops, nested loops, and dealing with finite series (an upper limit of a fixed integer).

Summation notation

When writing a summation notation we should be able to get back to the expanded sequence easily from the shorthand notation.

Given a sequence: am, am+1, am+2, ..., an

Sum of the terms of a sequence: am + am+1 + am+2 + ... + an

The sum of a finite series would be a partial sum of the sequence.

\sum_{k=m}^n a_k

This is commonly known as the sigma notation for the summation shorthand, where:

• k is the index
• m is the lower limit
• n is the upper limit
• Our index increments 1 at a time from m -> n
• a sub k is the value at the index

Example: Summation for - 1^2 - 2^2 + 3^2 - 4^2 + 5^2 - 6^2 + 7^2

= \sum_{k=1}^7 (-1)^{k+1} * k{2}

Example: Summation for - 3^3 + 3^4 + ... + 3^40

= \sum_{k=3}^40 3{k}

Closed form formula for calculating summations in progressions

This ensures we're able to easily add summations together for large sequences.

Example: For k = 1 to 100 do computation requiring k units of time.

time units at iteration k: ak = k (sub k)

a1 + ... + a100 is the same as:

= \sum_{k=1}^100 a_k = \sum_{k=1}^100 k

Summation of arithmetic progressions

Using the example above, we can use the following to easily calculate our total.

\sum_{k=1}^n k = ((n+1) * n)/2

Answer to the above:

((100 + 1) * 100)/2 = 5050

Summations in geometric progression

Within a binary tree, we can determine summations based on the depth.

Binary tree example to calculate node totals:

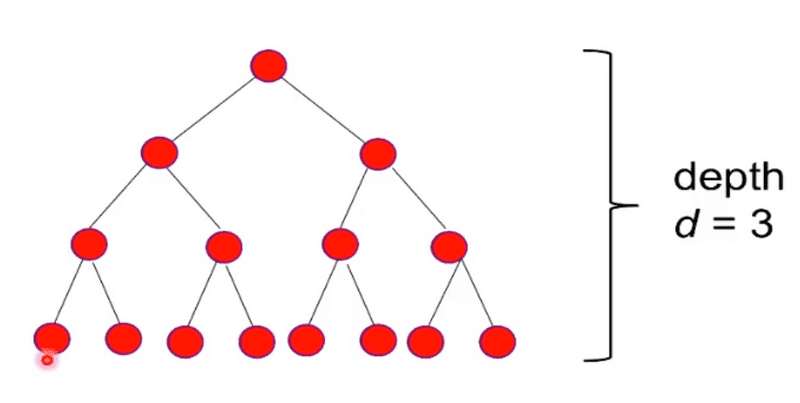
Example: How many nodes are in a depth of 3 in a balanced binary tree?

nodes at layer k: ak = 2^k

a0 + ... + ad is the same as:

\sum_{k=0}^d k = \sum_{k=0}^d 2{k}

Closed form formula for geometric progression summations

We can utilize the below generic formula for determining the sum of a geometric progression.

\sum_{k=0}^n r{k} = (r{n+1} - 1)/(r - 1)

The above example would be:

(2^(3 + 1) - 1)/(2 - 1)) = 15

Properties of sum transformations (changing sums)

We can change summation notations to split out nested sums to provide clarity.

Splitting two summations

If we have two or more summations together with the same constants we can handle them separately.

\sum_{k=m}^n (a_k + b_k) = \sum_{k=m}^n a_k + \sum_{k=m}^n b_k

Multiplying by a constant factor

When multiplying we can pull the factor out then multiply afterward.

\sum_{k=m}^n ca_k = c * \sum_{k=m}^n a_k

The sum of constant terms

When utilizing a constant we can determine the summation of the constant's terms by utilizing the below.

\sum_{k=m}^n c = c(n - m + 1)

Subtracting extra terms

We can subtract the extra terms from one summation to get another summation.

\sum_{k=m}^n a_k = \sum_{k=1}^n a_k - \sum_{k=1}^m-1 a_k

Example: We can determine the summation of the below by creating 2 summations, then subtracting the difference.

\sum_{k=5}^10 k = \sum_{k=1}^10 k - \sum_{k=1}^4 k

The above is now transformed to the closed forms:

= (10(10 + 1))/2 - (4(4 + 1))/2

Adding or subtracting numbers to indexes/limits to work with it easier

We can change the values of our upper/lower limits by a constant (the same for each) to make the value of the total easier to work with.

\sum_{k=m}^n a_k = \sum_{j=m+l}^n+l a_{j-l}

Example:

\sum_{k=5}^10 k, Say j = k - 4, k=j + 4

\sum_{j=1}^6 (j + 4) = \sum_{j=1}^6 j + \sum_{j=1}^6 4

The above is now:

= (6(6 + 1))/2 + 4 * (6 - 1 + 1)

The telescoping sum in summations

If a summand can be expressed as a difference of two terms, then we can have a cascade of cancellations that greatly simplifies our end formula.

\sum_{k=1}^n (a_k - a_{k+1}) = a_1 - a_{n+1}

Note: We can rewrite our summands to reach this.

Example:

\sum_{k=1}^n (1/(n(n+1)))

= \sum_{k=1}^n ((1/n) - (1/(n + 1)))

= (1/1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + ... + (1/(n-1) - 1/n) + (1/n - (1/(n + 1)))

Exploring double sums, nested summations

These are similar to nested for loops. We have to compute the inner summation, then calculate the outer summation.

\sum_{i=1}^n \sum_{j=1}^m a_{ij} = \sum_{i=1} a_{i1} + a_{i2} + ... + a_{im}

Example:

\sum_{i=1}^3 \sum_{j=1}^2 ij = \sum_{i=1} (i * 1 + i * 2) = \sum_{i=1}^3 3i = 3 * 3(3 + 1)/2 = 18