weak mathematical induction

Weak mathematical induction is a proof technique designed to prove statements about all natural numbers.

This is different than inductive reasoning, which uses repeated observations to support a hypothesis.

Mathematical induction instead gives definitive proof, using smaller cases to build upon each other and prove larger cases.

Note: This requires lots of algebra.

Useful symbols: ≥ ≤ = ¬ ∼ ∧ ∨ ⊕ ≡ → ↔ ∃ ∀

Mathematical induction

• More recently developed proof technique
• It does not generate answers it can only prove them

Weak induction

• Principle of weak mathematical induction:
  • Let P(n) be a property that is defined for integers n and let a be
  some integer. If the following statements are true: * P(a) is true * ∀ k ≥ a, P(x) → P(k + 1) * Then the following conclusion is also true: "For every integer n ≥ a, P(n)"

This is a two step process (basis and inductive).

Steps for a weak induction

1. Introduction
   1. State the property precisely:
      • "For every integer n ≥ a the property P(n) is true"
2. Proof (by mathematical induction)
   1. Show the basis step is true:
      • P(a) is true because ...
   2. State the inductive hypotehsis clearly:
      • Assume P(k) is true, where k is any particular but arbitrary integer with k ≥ a
   3. Show that the inductive step is true:
      • Assuming the inductive hypothesis P(k), prove that P(k + 1) holds;
        • proving: ∀ k ≥ a, P(k) → P(k + 1)
3. Conclusion:
   1. State the conclusion precisely:
      1. Since we have proved the basis step and inductive step, we conclude that
      the proposition is true.

Example: Prove that algorithm A correctly sorts anyf inite list of numbers.

• P(n) ≡ A is correct for any list of length n
• Prove that ∀ n P(n) for domain of non-negative integers
  • We want to prove that the problem is provable

Example of weak induction

Prove that for any positive integer n

1 + 2 + ... + n = ((n+1)*n)/2

• P(n) ≡ sum(i) i=1, n ≡ ((n+1)*n)/2
• "For every integer n ≥ 1 the property P(n) is true"

Weak mathematical induction proof:

• Basis step - prove P(1) is true

• Inductive step - prove the implication ∀ k ≥ 1, P(k) → P(k + 1)

• Basis step: P(1) is true

  • Left hand side (sum side): = 1
  • Right hand side: ((1 + 1) * 1)/2 = 1
  • We've proven P(1) holds true

Screenshot to avoid confusion with the lack of formula support:

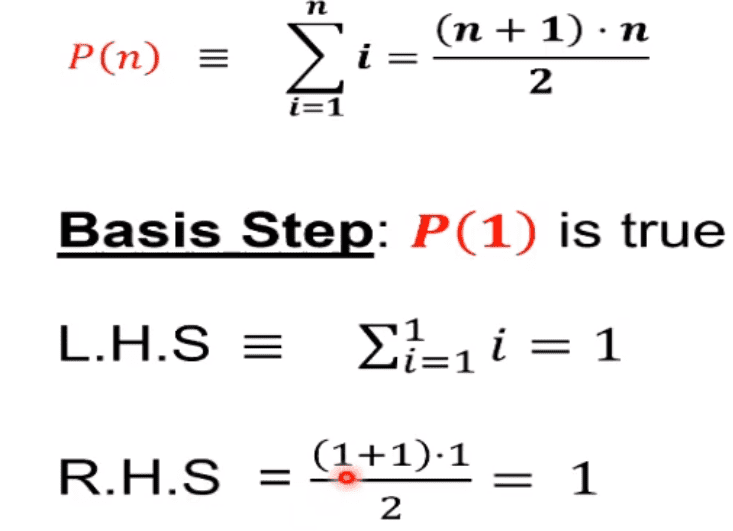
• Inductive step - prove the implication ∀ k ≥ 1, P(k) → P(k + 1)
  • We can try the direct proof approach, for most cases it will work
  • If we know P(k) is true, then we get ((k + 1) * k)/2
    • Basically the same equation, with k in it
  • To prove P(k + 1) is true:
    • ((k + 2)*(k + 1))/2
    • Note that we only have a difference of our previous statement in this + 1 term
      • Often when working with the sum, we now want to rewrite this in terms of the hypothesis
      • ((k + 1) * k)/2 + ((k + 1) * 2)/2
      • Now factor common expressions
      • (k + 1)/2 * (k + 2)
      • = ((k + 2) * (k + 1))/2
  • We can prove now that P(k + 1) holds true

Example of weak induction

Prove using mathematical induction that for all n ≥ 2, n^3 - n is divisible by 6

P(n) == 6 | n^3 - n or n^3 - n = 6m, m is some integer

• For every integer n ≥ 2, the property P(n) is true

• Basis step: P(2) is true

• Inductive step: prove the implication ∀ k ≥ 1, P(k) → P(k + 1)

• Basis step: P(2) is true

2^3 - 2 = 8 - 2 = 6 which is clearly divisible by 6 This proves that the basis is true

• Inductive hypothesis: P(k) is true, k ≥ 2

P(k) == 6 | k^3 - k or k^3 - k = 6q, q is some ikteger * We're rewriting using our proven basis step

• Inductive step: we now prove P(k + 1) is true

P(k + 1) == 6 | (k + 1)^3 - (k + 1) or (k + 1)^3 - (k + 1) = 6m', 6m' is some integer

P(k + 1) == (k + 1)^3 - (k + 1) == k^3 + 3k^2 + 3k + 1 - k - 1 == (k^3 - k) + (3k^2 + 3k) == (k^3 - k) + 3k(k + 1)

• We can now substitute our k^3 - k for our equivalent value

== 6q + 3k(k + 1) (by inductive hypothesis step) == 6q + 3 * 2r where k(k + 1) = 2r, r is some integer by the product of 2 consecutive integers always being even == 6q + 6r == 6(q + r) == 6m', using the closure property as some integer m', where q+r is an integer because the sum of integers is an integer

This holds to be true, it is equivalent.

Example of weak induction

Prove using mathematical induction that for all n ≥ 0, 1 + 3n ≤ 4^n

P(n) == 1 + 3n ≤ 4^n For every integer n ≥ 0, the property P(n) is true

• Basis step: prove P(0) is true

• Inductive step: prove the implication ∀ k ≥ 0, P(k) → P(k + 1)

• Basis step: P(0) is true

P(0) == 1 + 3(0) ≤ 4^0 == 1 + 0 ≤ 1 == 1 ≤ 1

• Inductive hypothesis: P(k) is true, k ≥ 0

P(k) == 1 + 3k ≤ 4^k is true

• Inductive step: P(k + 1) is true

P(k + 1) == 1 + 3(k + 1) ≤ 4^(k + 1)

Right hand side: 4^(k+1) = 4 * 4^k = (3 + 1) * 4^k = 3 * 4^k + 4^k Left hand side: 1 + 3(k + 1) = (1 + 3k) + 3

(1 + 3k) + 3 ≤ 4^k + 3 ≤ 4^k + 3*4^k

We know that this will always be true: 3 ≤ 3*4^k, k ≥ 0

We can conclude these are true.