asymptotic notation of algorithms

Asymptotic is the behavior of a line as itt approaches a curve but never touches it. In analyzing efficiency we want to know how running time increases as size of input increases without bound. This uses big-O, omega, and theta.

This is where T(n) and g(n) can be any nonnegative functions defined as positive integers.

• T(n) - running time
• g(n) - Some simple function to compare T(n) with

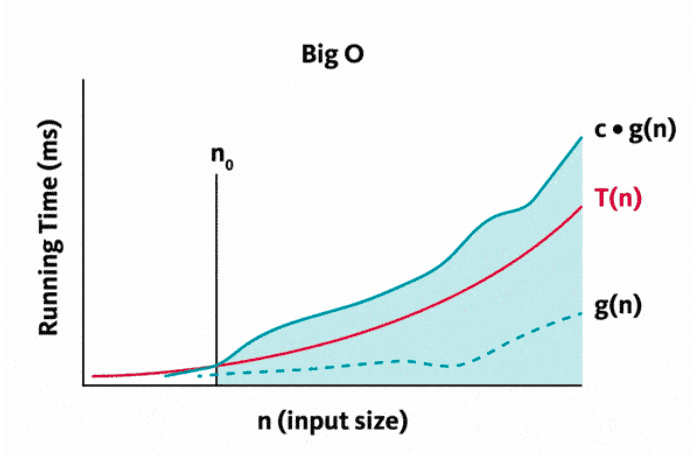
O Notation (Big O)

Informally, O(g(n)) is a set of all functions with a lower or same order og frowth as g(n) within a constant multiple, as n goes to infinity.

We can say T(n) is O(g(n)) if T(n) exists in O(g(n))

This can be expressed graphically, where c is a positive constant

Formal expression:

• A function T(n) is said to be in O(g(n)), denoted by

T(n) ∈ O(g(n)), if T(n) ≤ c(g(n)) for all n ≥ n0, for some positive constant c.

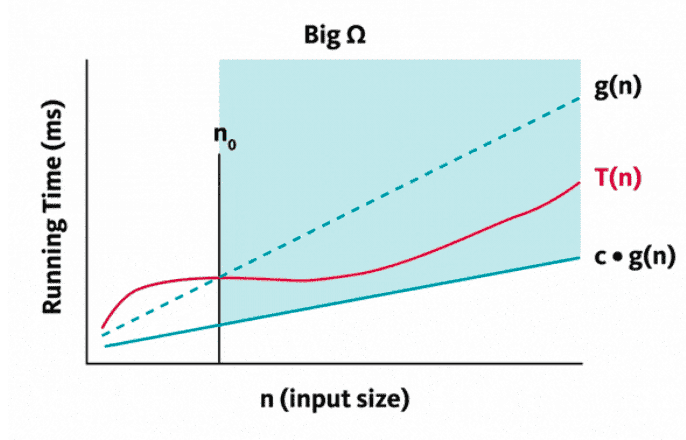
Ω Notation (Omega)

Informally, Ω(g(n)) is a set of all functions with a higher or same order of growth as g(n) (within a constant multiple, as n goes to infinity). we say a function T(n) “is Ω(g(n))” if T(n) ∈ Ω(g(n)).

This can be expressed graphically, where c is a positive constant

Formal expression:

• A function T(n) is said to be in Ω(g(n)), denoted by

T(n) ∈ Ω(g(n)), if T(n) ≥ c(g(n)) for all n ≥ n0 , for some positive constant c.

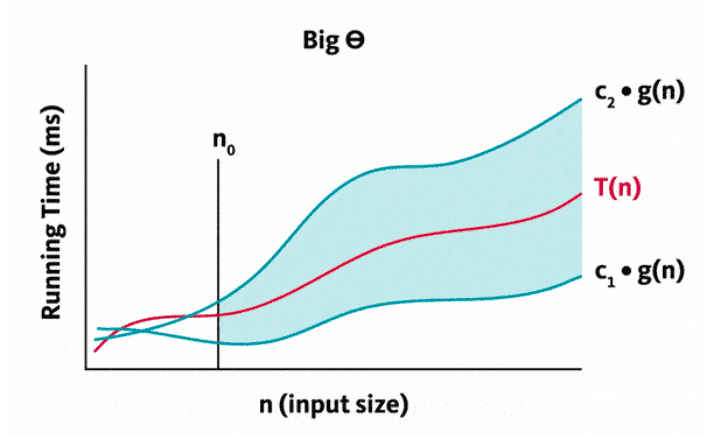
Θ Notation (Theta)

Informally, Θ(g(n)) is a set of all functions that have the same order of growth as g(n) ( bounded both above and below by some positive constant multiples of g(n), as n goes to infinity)

We say a function T(n) “is Θ(g(n))” if T(n) ∈ Θ(g(n)).

This can be expressed graphically, where c is a positive constant

Formal expression:

• A function T(n) is said to be in Θ(g(n)), denoted by T(n) ∈ Θ(g(n)), if c1 g(n) ≤ T(n) ≤ c2 g(n) for all n ≥ n0,

for some positive constants c1 and c2.

This seems to be a wavier graph that might have tigher bounds (more accurate?).

Comparing orders of growth

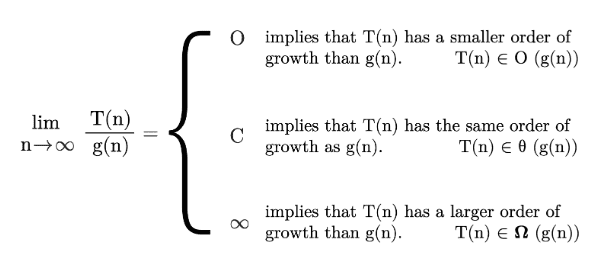
We can use formal definitions of O, omega, and theta but computing the limit of the ratio of 2 functions is more convenient.

Limits example shown here:

The limit based approach is convenient because it benefits from techniques in calculus.

Note:

• f(n)∈ Θ(g(n)) implies f(n) = O(g(n)) and f(n) = Ω(g(n)) since theta notation

is stronger notation than O- and Ω-notation

Properties involving asymptotic notations

f(n) ∈ Θ(g(n)) O(g(n)) Ω(g(n))

• Transitivity
  • f(n) = Θ(g(n)) and g(n) = Θ(h(n)) imply f(n) = Θ(h(n))
  • f(n) = O(g(n)) and g(n) = O(h(n)) imply f(n) = O(h(n))
  • f(n) = Ω(g(n)) and g(n) = Ω(h(n)) imply f(n) = Ω(h(n))
• Reflexivity
  • f(n) = Θ(f(n))
  • f(n) = O(f(n))
  • f(n) = Ω(f(n))
• Symmetry
  • f(n) = Θ(g(n)) if and only if g(n) = Θ(f(n))
• Transpose symmetry
  • f(n) = O(g(n)) if and only if g(n) = Ω(f(n))